頂垂線 (三角形)
初等幾何学における三角形の頂垂線(ちょうすいせん、英: altitude)または単に垂線は、その三角形のひとつの頂点からその対辺(この場合、その頂点に対する「底辺」と呼ぶ)を含む直線へ垂直に引いた線分を言う[注釈 1]。この対辺を含む直線のことを、その頂点または頂垂線に対する「延長された底辺」(extended base)あるいは「底辺の延長(線)」と呼ぶ[注釈 2]。(頂)垂線と底辺(の延長線)との交点は、(頂)垂線の足(foot)と言う。頂垂線の「長さ」(しばしばこれを「高さ」〈"the altitude"〉と呼ぶ)は、頂点と底辺(の延長線)との間の距離(すなわち、頂点とそこから引いた頂垂線の足との間の距離)を言う。頂点から頂垂線をその足まで描くことを、頂点から「垂線を降ろす」(dropping the altitude)と言い、それは直交射影の特別の場合である。
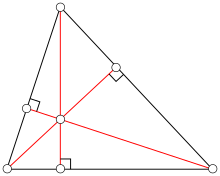
高さは三角形の面積の計算にも用いることができる: 三角形の面積は、底辺の長さと頂垂線の長さの積の半分に等しい。したがって、三角形の最長の頂垂線は最短辺に垂直である。また、頂垂線と各辺は三角函数を通じて関係している。

二等辺三角形(二つの合同な辺を持つ三角形)において、合同でない辺を底辺として持つ頂垂線は、その辺の中点を足に持つ。また合同でない辺を底辺とする頂垂線は、その頂角の二等分線である。
頂垂線またはその長さを表すのにしばしば文字 h(height に由来) が用いられ、対応する頂点を表す記号をしばしば添字として付けてどの頂点からの垂線なのかを表す。
直角三角形において、直角を持つ頂点から斜辺 c へ引いた垂線によって斜辺を二つの線分(それぞれ長さ p および q)に分割する。この頂垂線の長さを hc と書けば、 なる関係が成り立つ(幾何平均定理)。

鋭角三角形および直角三角形に対しては、すべての頂垂線の足は三角形の(延長線上でない)辺上に載っている。(一つの鈍角を含む)鈍角三角形においては、鈍角を持つ頂点からの垂線は対辺の内部に足を降ろすが、残りの鋭角を持つ二頂点からの垂線はそれぞれの対辺の延長線上(すなわち三角形の外)に足を降ろす。
-
三角形の各辺を頂垂線との交点で分割し、分割後のそれぞれの長さの辺を持つ正方形を作り(6つ)、図のように時計回りに赤・青・赤・青・赤・青とグループ分けして、赤と青の面積を求めると、両面積は等しくなっている(カルノーの定理の特別な場合)。
-
三角形においては、頂垂線(或いはその延長線)上における垂心から足まで長さと足から三角形の外接円と延長線上の交点(当該頂垂線が関わる頂点ではない側)までの長さが一致する。図の中の外接円が書かれた黄色の三角形の各辺の両側にある赤・青・緑の領域は、それぞれ辺を軸とする線対称な形となっている。
-
ある三角形の頂垂線の足3箇所を円周上に持つ正円について、その円周上には同じ三角形の各辺を二等分する点3箇所も存在し、その面積は同じ三角形の外接円の面積の4分の1となっている。
-
三角形の三辺の位置と長さそのものを直径とする三つの円によって生じる3本の共通弦は、その三角形の3本の頂垂線となる。
-
三角形の一辺が頂垂線の足で分割される場合、分割後の長さの辺を持つ正方形同士の面積の差分は、当該三角形の他の二辺で作られる正方形同士の面積の差分と等しくなっている。
-
鋭角三角形(橙)の各辺を用いた各正方形を係る辺の向かいの頂点からの頂垂線の延長線で分割した場合、分割後に生じる長方形について同色のもの同士の面積は互いに等しくなっている。
垂心
編集三角形の三つの頂垂線(場合によってはその延長線)は、三角形の垂心 H と呼ばれる一点において交わる。[1][2]。垂心が三角形の内部にあるための必要十分条件はその三角形が鋭角三角形(すべての角が直角以上になることがない三角形)となることである。一つの角が直角ならば、垂心はその直角を成す頂点に一致する[2]。
三角形の頂点およびそのなす角を同じ文字 A, B, C で表し、対応する辺の長さを a = |BC|, b = |CA|, c = |AB| とする(しばしば辺自体も同じ文字で表す)とき、垂心の三線座標は で与えられ[3]、また重心座標は で与えられる。
重心座標系は三角形の内点に対してすべての座標が正となるが、外部の点では少なくとも一つの座標が負であり、また頂点において二つの座標の値が零となるから、垂心に対して与えられる上記の重心座標は、垂心が鋭角三角形の内部にあり、直角三角形の直角を成す頂点上にあり、また鈍角三角形の外部にあることを示すものになっている。
ガウス平面において、点 A, B, C はそれぞれ複素数 zA, zB, zC を表現するものであり、三角形 ABC の外接円がガウス平面の原点に中心を持つと仮定すれば、複素数 を表現する点 H は三角形 ABC の垂心である[4](p. 90, Proposition 3)。これにより、垂心 H の自由ベクトルによる特徴付け が直接的に得られる。前者の式は「シルベスターの問題」と呼ばれるベクトルの等式で、ジェームス・ジョセフ・シルベスターが提案した[5]:142。
性質
編集三角形の各頂点 A, B, C から降ろした垂線の足をそれぞれ D, E, F と書けば:
- 一つの頂垂線を垂心によって分けた二つの線分の長さの積は、どの頂垂線に対しても等しい値となる:[6][7] この値の平方を半径とする H に中心を持つ円は、もとの三角形の極円である[8]。
- 三つの頂垂線に亘る、各頂垂線の長さに対する底面から垂心までの距離の比の和は、1 に等しい:[9] この性質と次の性質は、任意の内点とそれを通る三つのチェバ線に関するより一般の性質の応用である。
- 各頂垂線に対する垂心から頂点への長さの比を、三つの頂垂線に関して加えたものは 2 に等しい:[9]
- 垂心の等角共役はその三角形の外心である[10]
- 垂心の等長共役は反中点三角形の類似重心である[11]
- 平面上の四点で、そのうちの一点が残りの三点の成す三角形の垂心となっているような組を垂心系または垂心四角形 (orthocentric quadrangle) と言う。
円および円錐曲線との関係
編集三角形の外接半径を R とすれば が成り立つ[12][13]。
さらに外接半径 R とともに、三角形の内接半径を r, 傍接半径を ra, rb, rc とすれば、頂点から垂心への距離に関して以下の関係 が満足される[14]。
任意の頂垂線、例えば AD を延長して外接円と交わる点を P とし、外接円の弦 AP を作れば、その足 D は線分 HP を二等分する(すなわち )[7]。
三角形の一辺とほかの二辺の延長とに外接 (externally tangent) する任意の放物線の準線は、その三角形の垂心を通過する(シュタイナー線)[15][16]。
三角形の垂心を通る外接円錐曲線は直角双曲線である(ポンスレ束)[15][17]。
他の中心との関係
編集垂心 H, 重心 G, 外心 O, および九点円の中心 N はすべて同一直線上にあり、その直線はオイラー線と呼ばれる[18]。九点円の中心は垂心と外心を結ぶオイラー線の中点の位置にあり(したがって )、重心と外心の間の距離は重心と垂心との距離の半分に等しい( )[19]。
垂心は内心 I との距離が、重心との距離より小さく( )、また垂心は重心からの距離が内心よりも大きい( )。
三角形の三辺の長さ a, b, c, 内半径 r および 外半径 R を用いて、以下が成立する[20]:
- [21]:449
垂足三角形
編集三角形 ABC が斜三角形(直角を含まない)ならば、もとの三角形の垂心に関する垂足三角形 (pedal triangle) を、単にその三角形の垂足三角形 (orthic triangle, altitude triangle) と呼ぶ。つまり、斜三角形のすべての頂垂線の足の成す三角形 DEF が垂足三角形である。垂足三角形 DEF の内心は、もとの三角形 ABC の垂心に一致する[22](p. 292, See also: Corollary 5.5, p. 318)。
垂足三角形の頂点に対する三線座標系は以下で与えられる:
- D = 0 : sec B : sec C,
- E = sec A : 0 : sec C,
- F = sec A : sec B : 0.
垂足三角形の延長辺は、その基準三角形の対延長辺と三つの共線点で交わる[23][24][22]。
任意の鋭角三角形において、周長最小となる内接三角形はその垂足三角形である[25]。 これは1775年に提示されたファニャノの問題の解である[26]。垂足三角形の辺は、その外接円のもとの三角形の頂点における接線に平行である[27]。
鋭角三角形の垂足三角形は triangular light route を与える[28]。
三角形 ABC の各辺の中点における九点円の接線は、垂足三角形の辺に平行であり、垂足三角形に相似な三角形を成す[29]。
垂足三角形は外接三角形に近い関係を持つ。LA を三角形 ABC の頂点 A における外接円の接線とし、同様に各頂点に対して外接円の接線 LB, LC も定義する。三つの交点 A" ≔ LB ∩ LC, B" ≔ LC ∩ LA, C" ≔ LC ∩ LA の成す三角形 A"B"C" をもとの三角形の外接三角形と呼び、その辺は三角形 ABC の外接円に頂点 A, B, C において接する。この外接三角形は垂足三角形の中心相似形である。外接三角形の外心および、外接三角形と垂足三角形の相似の中心はオイラー線上にある[21]:447。
外接三角形の頂点の三線座標系は以下で与えられる:
- A" = −a : b : c;
- B" = a : −b : c;
- C" = a : b : −c.
垂足三角形に関するより詳細は垂心系#一般の垂足三角形の項を参照。
いくつかの垂線定理
編集辺の垂線定理
編集任意の三角形に対して、その辺の長さを a, b, c, 半周長を s = (a + b + c) / 2 と置けば、辺 a に対する頂垂線の長さは で与えられる。
これは三角形の面積を辺の長さで表すヘロンの公式と面積公式 (底辺)×(高さ)/2(を辺 a とその対角 A からの垂線に対して適用したもの)を組み合わせれば出る。
内半径定理
編集任意の三角形を考え、その辺の長さを a, b, c, 対応する頂垂線の長さをそれぞれ ha, hb, hc とするとき、これら頂垂線の長さと内半径 r は なる関係を持つ[30](Lemma 1)。
外半径定理
編集三角形の一辺 a に対応する頂垂線の長さを ha とし、残りの二辺の長さを b, c と置けば、その三角形の外半径 R によって、頂垂線の長さは で与えられる[31]。
内点
編集三角形の内点 P に対し、P から各辺への垂直距離をそれぞれ p1, p2, p3 とし、対応する辺における頂垂線の長さを h1, h2, h3 とすれば が成り立つ[32]。
面積定理
編集任意の三角形の三辺を a, b, c とそれぞれに対応する頂垂線の長さを ha, hb, hc と書けば、頂垂線の長さの逆数和の半分 に対して三角形の面積 Area は を満足する[33]。
垂線上の一般点
編集任意の三角形 ABC の頂垂線 AD 上の任意の点 E に対し が成り立つ[34]:77–78。
特別な三角形の場合
編集正三角形
編集正三角形内の任意の点 P に対し、三辺への垂線の長さの和はその三角形の頂垂線の長さに等しい。これはヴィヴィアーニの定理である。
直角三角形
編集直角三角形の三つの頂垂線の長さ ha, hb, hc(ただし前の二つはそれぞれの対辺への足の長さ b, a にそれぞれ等しいものとする)は なる関係を持つ[35][36]。
脚注
編集注釈
編集出典
編集- ^ Smart 1998, p. 156.
- ^ a b Berele & Goldman 2001, p. 118.
- ^ Clark Kimberling's Encyclopedia of Triangle Centers “Archived copy”. 2012年4月19日時点のオリジナルよりアーカイブ。2012年4月19日閲覧。
- ^ Andreescu, Titu; Andrica, Dorin (2006), Complex numbers from A to...Z, Boston: Birkhäuser, ISBN 978-0-8176-4326-3
- ^ Dörrie, Heinrich (1965), 100 Great Problems of Elementary Mathematics. Their History and Solution, New York: Dover Publications, ISBN 0-486-61348-8
- ^ Johnson 2007, p. 163, Section 255.
- ^ a b Orthocenter of a triangle
- ^ Johnson 2007, p. 176, Section 278.
- ^ a b Panapoi, Ronnachai, Some properties of the orthocenter of a triangle, University of Georgia
- ^ Smart 1998, p. 182.
- ^ Weisstein, Eric W. "Isotomic conjugate". mathworld.wolfram.com (英語).
- ^ Weisstein, Eric W. "Orthocenter". mathworld.wolfram.com (英語).
- ^ Altshiller-Court 2007, p. 102.
- ^ Bell, Amy (2006), “Hansen's right triangle theorem, its converse and a generalization”, Forum Geometricorum 6
- ^ a b 齋藤 輝. “等角共役とシムソン線の幾何学”. 角川ドワンゴ学園 N/S 高等学校研究部. 2024年4月29日閲覧。
- ^ Weisstein, Eric W. "Kiepert Parabola". mathworld.wolfram.com (英語).
- ^ Weisstein, Eric W. "Jerabek Hyperbola". mathworld.wolfram.com (英語).
- ^ Berle & Goldman 2001, p. 123.
- ^ Berele & Goldman 2001, pp. 124–126.
- ^ Gras, Marie-Nicole (2014), “Distances between the circumcenter of the extouch triangle and the classical centers”, Forum Geometricorum 14: 51-61
- ^ a b Smith, Geoff; Leversha, Gerry (November 2007), “Euler and triangle geometry”, Mathematical Gazette
- ^ a b William H. Barker, Roger Howe (2007). “§ VI.2: The classical coincidences”. Continuous symmetry: from Euclid to Klein. American Mathematical Society. ISBN 0-8218-3900-4
- ^ Johnson 2007, p. 199, Section 315.
- ^ Altshiller-Court 2007, p. 165.
- ^ Johnson 2007, p. 168, Section 264.
- ^ Berele & Goldman 2001, pp. 120–122.
- ^ Johnson 2007, p. 172, Section 270c.
- ^ Bryant, V., and Bradley, H., "Triangular Light Routes," Mathematical Gazette 82, July 1998, 298-299.
- ^ Kay, David C. (1993), College Geometry / A Discovery Approach, HarperCollins, p. 6, ISBN 0-06-500006-4
- ^ Andrica, Dorin; Marinescu, Dan Sțefan (2017), “New Interpolation Inequalities to Euler’s R ≥ 2r”, Forum Geometricorum 17: 149–156
- ^ Johnson 2007, p. 71, Section 101a.
- ^ Johnson 2007, p. 74, Section 103c.
- ^ Mitchell, Douglas W. (November 2005), “A Heron-type formula for the reciprocal area of a triangle”, Mathematical Gazette 89: 494
- ^ Posamentier, Alfred S.; Salkind, Charles T. (1996), Challenging Problems in Geometry (second revised edition ed.), Dover Publishing
- ^ Voles, Roger (July 1999), “Integer solutions of ”, Mathematical Gazette 83: 269–271
- ^ Richinick, Jennifer (July 2008), “The upside-down Pythagorean Theorem”, Mathematical Gazette: 313–317
参考文献
編集- Altshiller-Court, Nathan (2007) [1952], College Geometry, Dover Publications
- Berele, Allan; Goldman, Jerry (2001), Geometry / Theorems and Constructions, Prentice Hall, ISBN 0-13-087121-4
- Johnson, Roger A. (2007) [1960], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
- Smart, James R. (1998), Modern Geometries (5th ed.), Brooks/Cole, ISBN 0-534-35188-3
関連項目
編集外部リンク
編集- Weisstein, Eric W. "Altitude". mathworld.wolfram.com (英語).
- Orthocenter of a triangle With interactive animation
- Animated demonstration of orthocenter construction Compass and straightedge.
- Fagnano's Problem by Jay Warendorff, Wolfram Demonstrations Project.






