菱形三十面体
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
菱形三十面体(りょうけいさんじゅうめんたい、英: rhombic triacontahedron)とは、カタランの立体の一種で、二十・十二面体の双対多面体である。また、ゾーン多面体、等面菱形多面体の一種でもある。正十二面体または正二十面体の各面の中心を持ち上げ、隣り合う三角形同士が同一平面上となるようにした形にもなっている。
| 菱形三十面体 | |
|---|---|
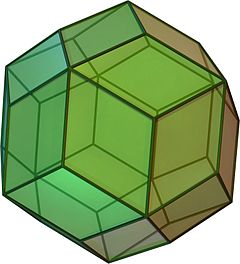  | |
| 種別 | カタランの立体、等面菱形多面体、三十面体 |
| 面数 | 30 |
| 面形状 |
菱形の一種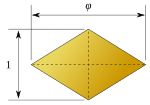 |
| 辺数 | 60 |
| 頂点数 | 32 |
| 対称群 | Ih |
| 双対多面体 | 二十・十二面体 |
| 特性 | 凸集合 |
全ての目が同じ条件であるため、三十面のサイコロには最もよく使われている。
一部の菱形10枚を抜くことにより菱形二十面体が生成される。
性質
編集近縁な立体
編集関連項目
編集外部リンク
編集- Weisstein, Eric W. "Rhombic Triacontahedron". mathworld.wolfram.com (英語).
