2部グラフ
(二部グラフから転送)
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
数学、特にグラフ理論における2部グラフ(にぶグラフ、英: bipartite graph)とは、頂点集合を2つに分割して各部分の頂点は互いに隣接しないようにできるグラフのことである。一般に互いに隣接しない頂点からなる集合を独立集合といい、頂点集合を n 個の独立集合に分割可能なグラフのことを n 部グラフ (n-partite graph) という。

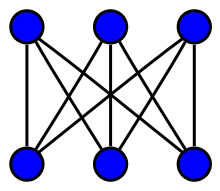
頂点集合を独立集合 V1, V2 に分割したとき、V1 と V2 の任意の頂点が隣接するグラフを完全2部グラフという。頂点集合が m 頂点とn 頂点に分割される完全2部グラフを Km,n と書く。
辺を共有する頂点を異なる色で塗ることを(頂点)彩色という。よって、n 部グラフは n 彩色可能なグラフに他ならない。同様に、頂点を共有する辺を異なる色で塗ることを辺彩色という。
2部グラフの辺集合はどの2辺も互いに隣接していないときマッチングと呼ばれる。辺の数が最大のマッチングを最大マッチングと呼ぶ。また、すべての頂点がマッチングに含まれる辺の端点であるとき完全マッチングと呼ぶ。