バトラー・ボルマー式
バトラー・ボルマー式(バトラー・ボルマーしき、英: Butler–Volmer equation)または Erdey-Grúz–Volmer 式とは、電気化学反応速度論における最も基礎的な関係式である。同じ電極上でカソード反応とアノード反応の両方が起きるとした上で、電極に流れる電流が次のように電極電位に依存することを主張する。
または、次のように簡便化して書くこともできる。
ここで、次のような変数を用いた。
- j: 電極電流密度 A/m2 (j = I/A)
- j0: 交換電流密度 A/m2
- E: 電極電位 V
- Eeq: 平衡電位 V
- T: 絶対温度 K
- z: 電極反応に関わる電子数
- F: ファラデー定数
- R: 気体定数
- αc: いわゆるカソード電荷移動係数: 無次元数
- αa: いわゆるアノード電荷移動係数: 無次元数
- η: 活性化過電圧 (η = E − Eeq)
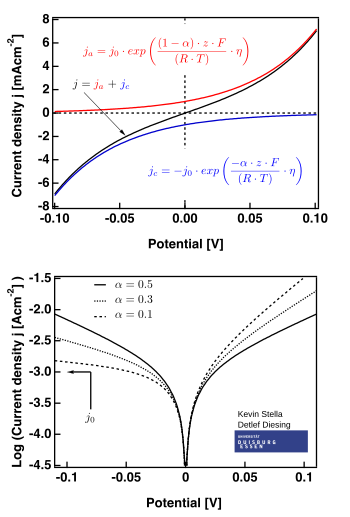
右図のプロットは αa=1 − αc が成り立つものとしている。
この式の名称は、ジョン・アルフレッド・バレンタイン・バトラー[1]とマックス・フォルマー (Max Volmer)に由来する。
物質輸送律速
編集前述した形式のバトラー・ボルマー式は電極反応が電荷移動律速の場合、すなわちバルク電解質と電極表面との間の物質輸送が十分に速い場合にのみ成り立つ。しかし、電気化学においてバトラー・ボルマー式は広く有用であり、しばしば「現象論的電極反応速度論における中心的な方程式」 "central in the phenomenological electrode kinetics" であると言及される[2][3]。
限界電流の領域では、電極反応の中で物質輸送過程が律速段階であり、電流密度は以下のように記述される。
ここで、次の変数を用いた。
上式は電極表面における濃度とバルク電解質における濃度が等しい場合に(先に述べた)典型的な式と一致する。
極限
編集バトラー・ボルマー式には次の二つの極限が考えられる。
- 過電圧が低い領域(E ≈ Eeq)ではバトラー・ボルマー式は次のように単純化され、係数は「分極抵抗」と呼ばれる。
- 過電圧が高い領域ではバトラー・ボルマー式はターフェル式に単純化される。
- E ≪ Eeq の場合、カソード反応と一致
- E ≫ Eeq の場合、アノード反応と一致
ここで、a および b は(反応と温度で決まる)定数であり、ターフェル定数と呼ばれる。これらの理論的値はカソード反応とアノード反応とで異なる。
関連項目
編集出典
編集- ^ Mayneord, W. V. (1979). “John Alfred Valentine Butler. 14 February 1899-16 July 1977”. Biographical Memoirs of Fellows of the Royal Society 25: 144–126. doi:10.1098/rsbm.1979.0004.
- ^ J. O'M. Bockris; A.K.N.Reddy; M. Gamboa-Aldeco (2000). Modern Electrochemistry 2A. Fundamentals of Electrodics (Second Edition ed.). Kluwer Academic/Plenum Publishers. p. 1083
- ^ Samira Bagheri, Iraj Sadegh Amiri, Amin Termeh Yousefi, Sharifah Bee Abd Hamid "Nanocomposites in Electrochemical Sensors" (2017,CRC Press/Balkema) p.22
![{\displaystyle j=j_{0}\cdot \left\{\exp \left[{\frac {\alpha _{\mathrm {a} }zF}{RT}}(E-E_{\mathrm {eq} })\right]-\exp \left[-{\frac {\alpha _{\mathrm {c} }zF}{RT}}(E-E_{\mathrm {eq} })\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8807ffa6727108046fb98943ef950761af43eeb1)
![{\displaystyle j=j_{0}\cdot \left\{\exp \left[{\frac {\alpha _{\mathrm {a} }zF\eta }{RT}}\right]-\exp \left[-{\frac {\alpha _{\mathrm {c} }zF\eta }{RT}}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4afa357a095eba08cd05dfb36deb354a1b22dcdd)