冪集合 (べきしゅうごう、英 : power set )とは、数学 において、与えられた集合 から、その部分集合 の全体として新たに作り出される集合のことである。べき は冪乗 の冪(べき)と同じもので、冪集合 と書くのが正確だが、一部分をとった略字として巾集合 とも書かれる。
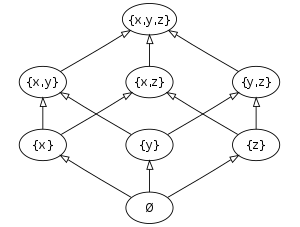
S = {x , y , z } の冪集合 P (S ) = { Φ , {x }, {y }, {z }, {x , y }, {y , z }, {z , x }, {x , y , z } } のハッセ図 。要素数は 23 = 8 である。集合と呼ぶべき対象を公理的にかつ構成的に与える公理的集合論 では、新たに作られた原体の冪集合もしくはそれに準ずる複数の冪集合が、それぞれの連続性に関わらず集合と呼ばれるべきもののうちにあることを公理の一つ(冪集合公理 )としてしばしば提示する。
集合
S
{\displaystyle S}
power からとって、通常は
P
(
S
)
,
P
(
S
)
,
p
o
w
(
S
)
,
P
o
w
e
r
(
S
)
,
Π
(
S
)
,
P
(
S
)
{\displaystyle {\mathfrak {P}}(S),\ {\mathcal {P}}(S),\ {\mathfrak {pow}}(S),\ \mathrm {Power} (S),\ \Pi (S),\;\mathbb {P} (S)}
℘ (S ), 2S などのように記される。2S X Y Y から X への写像 全体の集合を表すことによる(後述)。
集合 S が与えられたとき、S のすべての部分集合からなる集合
P
(
S
)
:=
{
A
:
a set
∣
A
⊆
S
}
{\displaystyle {\mathfrak {P}}(S):=\{A\colon {\mbox{a set}}\mid A\subseteq S\}}
を S の冪集合と呼ぶ。例えば
P
(
∅
)
=
{
∅
}
{\displaystyle {\mathfrak {P}}(\varnothing )=\{\varnothing \}}
P
(
{
a
}
)
=
{
∅
,
{
a
}
}
{\displaystyle {\mathfrak {P}}(\{a\})=\{\varnothing ,\{a\}\}}
P
(
{
x
,
y
}
)
=
{
∅
,
{
x
}
,
{
y
}
,
{
x
,
y
}
}
{\displaystyle {\mathfrak {P}}(\{x,y\})=\{\varnothing ,\{x\},\{y\},\{x,y\}\}}
P
(
{
1
,
2
,
3
}
)
=
{
∅
,
{
1
}
,
{
2
}
,
{
3
}
,
{
1
,
2
}
,
{
1
,
3
}
,
{
2
,
3
}
,
{
1
,
2
,
3
}
}
{\displaystyle {\mathfrak {P}}(\{1,2,3\})=\{\varnothing ,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}}
などとなる。空集合 の冪集合は空集合を唯一つの元として持つ一元集合 であり、空集合とは別のものである。
なおこの定義から明らかに
A
∈
P
(
S
)
⟺
A
⊂
S
{\displaystyle A\in {\mathfrak {P}}(S)\iff A\subset S}
である。
冪集合は包含関係 を順序として順序集合 になる。冪集合を底となる集合、包含関係を順序とする順序集合
(
P
(
S
)
,
⊂
)
{\displaystyle ({\mathcal {P}}(S),\subset )}
⊂
{\displaystyle \subset }
順序同型 な順序集合は単体様半順序集合 (simplex-like Poset) と呼ばれ、単体 の一つの組合せ論的な特徴づけを与える(底となる
P
(
S
)
{\displaystyle {\mathcal {P}}(S)}
P
(
S
)
{\displaystyle {\mathcal {P}}(S)}
⊂
o
p
p
{\displaystyle \subset ^{\mathrm {opp} }}
A
⊂
o
p
p
B
⟺
A
⊃
B
{\displaystyle A\subset ^{\mathrm {opp} }B\iff A\supset B}
を与えた順序集合
(
P
(
S
)
,
⊂
o
p
p
)
{\displaystyle ({\mathcal {P}}(S),\subset ^{\mathrm {opp} })}
(
P
(
S
)
,
⊂
)
{\displaystyle ({\mathcal {P}}(S),\subset )}
補集合 をとる操作
(
P
(
S
)
,
⊂
o
p
p
)
∋
A
⟼
≃
A
c
=
S
∖
A
∈
(
P
(
S
)
,
⊂
)
{\displaystyle ({\mathcal {P}}(S),\subset ^{\mathrm {opp} })\ni A\ {\stackrel {\simeq }{\longmapsto }}\ A^{c}=S\smallsetminus A\in ({\mathcal {P}}(S),\subset )}
によって与えられる。またこの対応で、集合の結び と交わり が互いに入れ替わる(双対性:ド・モルガンの法則 )、対称差 は不変(自己双対性)などを見て取ることができる。
順序集合
(
P
(
S
)
,
⊂
)
{\displaystyle ({\mathcal {P}}(S),\subset )}
M
⊂
P
(
S
)
{\displaystyle {\mathfrak {M}}\subset {\mathcal {P}}(S)}
が与えられたとき、集合族の結び や交わり をとる操作
sup
(
M
)
=
⋃
M
=
⋃
m
∈
M
m
,
inf
(
M
)
=
⋂
M
=
⋂
m
∈
M
m
{\displaystyle \sup({\mathfrak {M}})=\bigcup {\mathfrak {M}}=\bigcup _{m\in {\mathfrak {M}}}m,\quad \inf({\mathfrak {M}})=\bigcap {\mathfrak {M}}=\bigcap _{m\in {\mathfrak {M}}}m}
は、この集合族に対して包含関係による順序に関する上限と下限 を与える。とくに、
S
{\displaystyle S}
A
,
B
{\displaystyle A,B}
A
∨
B
:=
sup
{
A
,
B
}
=
A
∪
B
{\displaystyle A\vee B:=\sup\{A,B\}=A\cup B}
A
∧
B
:=
inf
{
A
,
B
}
=
A
∩
B
{\displaystyle A\wedge B:=\inf\{A,B\}=A\cap B}
を考えることにより、組
(
P
(
S
)
,
∧
,
∨
)
{\displaystyle ({\mathcal {P}}(S),\land ,\lor )}
完備束 となる。完備束の条件は空で無い部分集合族に対する上限・下限の存在を要求するものであるが、冪集合の束では集合族
M
⊂
P
(
S
)
{\displaystyle {\mathfrak {M}}\subset {\mathcal {P}}(S)}
sup
(
∅
)
=
∅
,
inf
(
∅
)
=
S
{\displaystyle \sup(\varnothing )=\varnothing ,\quad \inf(\varnothing )=S}
が冪集合
P
(
S
)
{\displaystyle {\mathcal {P}}(S)}
冪集合に定義される様々な集合演算は、冪集合を代数系 として取り扱う手段を与えてくれる。たとえば、集合の結び
∪
{\displaystyle \cup }
交わり
∩
{\displaystyle \cap }
交換可能 で結合的 な演算であるから、半群 として冪集合を見ることができる。さらに、結びに関する中立元 は空集合
∅
{\displaystyle \emptyset }
S
{\displaystyle S}
(
P
(
S
)
,
∪
,
∅
)
{\displaystyle ({\mathcal {P}}(S),\cup ,\emptyset )}
(
P
(
S
)
,
∩
,
S
)
{\displaystyle ({\mathcal {P}}(S),\cap ,S)}
モノイド である。また、対称差
Δ
{\displaystyle \Delta }
(
P
(
S
)
,
Δ
)
{\displaystyle ({\mathcal {P}}(S),\Delta )}
補集合 を逆元にもつ群 になる。
結び
∪
{\displaystyle \cup }
∩
{\displaystyle \cap }
分配的 であるので、
(
P
(
S
)
,
∪
,
∩
)
{\displaystyle ({\mathcal {P}}(S),\cup ,\cap )}
環 の構造を見て取ることができる。とくに冪集合
P
(
S
)
{\displaystyle {\mathcal {P}}(S)}
(
P
(
S
)
,
∩
,
∪
,
c
,
∅
,
S
)
{\displaystyle (P(S),\cap ,\cup ,^{\mathrm {c} },\varnothing ,S)}
と考えたものはブール代数 の例を与える。一方、事実として、任意の有限ブール代数は有限集合 のべき集合が作るこのブール代数によって同型的に実現することができる。
S の部分集合 A とその指示関数
χ
A
{\displaystyle \chi _{A}}
S S から {0, 1}[ 脚注 1] S , {0, 1}) =: {0 ,1}S 一対一に対応 する。これは、S の元 a が部分集合 A に属するとき 1、属さないとき 0 をラベル付けすることで部分集合 A が特定できるということに対応する。したがって特に A の濃度 card(A ) が有限の値 n であるとき冪集合 2A A card(A ) = 2n E から有限集合 F への写像の総数は card(F )card(E ) となり、このことは E から F への写像全体のなす集合 を F E 2の冪 としての記法はこれの特別の場合にあたる。
冪集合の濃度は元の集合の濃度より常に大きい(カントールの定理 )。有限集合のときにはこれは自明である。一般の場合は、カントールの対角線論法 によって示される。
^ 集合論の慣例で、自然数 2 を集合 {0,1} と同一視している。