モノイド対象
圏論において、モノイド対象(モノイドたいしょう、英: monoid object)(M, μ, η) は、モノイド圏 (C, ⊗, I) が与えられたとき、C の対象 M および二つの射(乗法: μ: M ⊗ M → M および単位射: η: I → M の組を言う。ただし二つの射はそれぞれ、五角形図式
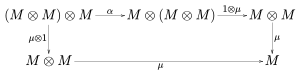
および単位子図式

を可換にするものでなければならない。上記の図式に現れる記号について、I はモノイド圏 C の ⊗ に対する(自然同型を除く)単位元であり、三つの射 α, λ, ρ はそれぞれ C における(自然同型を除く)結合律、左単位律、右単位律を与える射である。
モノイド圏 C におけるモノイド対象のことを、単にその圏の(内部)モノイドとも呼ぶ。これと双対的に、モノイド圏 C の余モノイド対象 (comonoid) は双対圏 Cop のモノイド対象を言う。
モノイド圏 C が対称(すなわち、自然同型を除く対称律を定める射 γ を持つ)ならば、C のモノイド対象 M が可換 (commutative) とは μ ∘ γ = μ となることを言う。
例
編集- 集合の圏 Set(に集合の直積をモノイド積とするモノイド圏の構造を入れたもの)におけるモノイド対象とは、通常の意味のモノイドである。
- 位相空間の圏 Top(に位相空間の直積をモノイド積としたもの)におけるモノイド対象は位相モノイドという。
- モノイドの圏 Mon(のモノイドの直積)に関するモノイド対象は、可換モノイドに他ならない。これはエックマン–ヒルトンの定理から容易に従う。
- 完備結び半束の圏 Sup(モノイド構造は半束の直積で入れる)のモノイド対象は単位的quantaleとなる。
- アーベル群の成すモノイド圏 (Ab, ⊗Z, Z) におけるモノイド対象は環である。
- 可換環 R に対し
- R-加群のモノイド圏 (R-Mod, ⊗R, R) のモノイド対象は R-結合多元環である。
- R-次数付き加群の圏におけるモノイド対象は次数付き R-多元環である。
- R-鎖複体の圏におけるモノイド対象は次数付き微分多元環である。
- ベクトル空間の圏 K-Vect(やはりテンソル積でモノイド構造を入れる)のモノイド対象はK-代数であり、余モノイド対象は K-余代数である。
- 任意の圏 C に対し、その自己函手の圏 [C,C] は函手の合成および恒等函手 IC の誘導するモノイド構造を持つ。このモノイド圏 [C,C] におけるモノイド対象は C のモナドである。
- 有限積持つ任意の圏に対し、任意の対象は対角射 ΔX: X → X を通じて余モノイド対象となる。双対的に、有限余積持つ任意の圏において、任意の対象は idX ⊔ idX: X ⊔ X → X を通じてモノイド対象となる。
モノイド対象の圏
編集モノイド圏 C の二つのモノイド対象 (M, μ, η) と (M′, μ′, η′) に対し、射 f: M → M′ がモノイド対象の射 (morphism of monoids) あるいはモノイド射 (monoid morphism) であるとは f ∘ μ = μ′ ∘(f ⊗ f) および f ∘ η = η′ を満たすときに言う。すなわち以下の図式
| および |
が可換となる。
圏 C における全てのモノイド対象とそれらの間の全てのモノイド射の成す圏をMonC などと書く[1]。この書き方で通常のモノイドの圏は Mon = MonSet と書ける。
関連項目
編集- Act-S: 集合へのモノイド作用 (action on set) の圏
参考文献
編集- ^ Section VII.3 in Mac Lane, Saunders (1988). Categories for the working mathematician (4th corr. print. ed.). New York: Springer-Verlag. ISBN 0-387-90035-7
- Mati Kilp, Ulrich Knauer, Alexander V. Mikhalov, Monoids, Acts and Categories (2000), Walter de Gruyter, Berlin ISBN 3-11-015248-7
外部リンク
編集- monoid in a monoidal category in nLab
- category of monoids in nLab (Mon(C))