ボヤイの定理（―のていり、Bolyai's theorem）またはボヤイ＝ゲルヴィンの定理 (Bolyai–Gerwien theorem）は、1833年にボーヤイ・ファルカシュによって示された『面積の等しい二つの多角形 A, B が存在した時、A を有限回分割し組みなおすことで、B と合同な図形を作ることが出来る』という定理である。
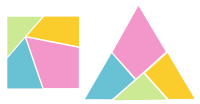分割された等積多角形の例（デュードニーの『カンタベリー・パズル』より「正三角形と正方形」[1]）
この問題を三次元に拡張した予想がヒルベルトの23の問題の第3問題に挙げられていたが、1900年に否定的に解決された。
