フラッシュ蒸留
フラッシュ蒸留(フラッシュじょうりゅう)は、気体と液体の分離手法。平衡フラッシュ蒸留ともいう[1]。減圧下で原液の一部を蒸発させ、気相と液相を平衡にした状態(気液平衡)でおこなう[1]。
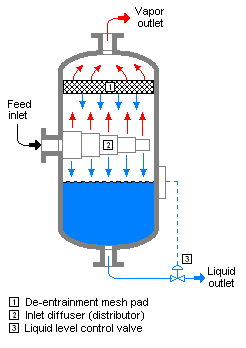
絞り弁または装置が圧力容器の入口に配置されており、フラッシュ蒸発が容器内で発生する場合、その容器はしばしばフラッシュドラムと呼ばれる[2][3]。
概要
編集何らかの飽和液(沸点に達している液体、飽和蒸気圧が気圧と釣り合っている状態、水なら100度)を圧力の低い環境に投入すると、即座に液体の一部が蒸気に気相と液相が平衡状態になる。この時、行われた操作をフラッシュ(英:Flash evaporation)と言い、生じた蒸気をフラッシュ蒸気、再蒸発蒸気という。
このフラッシュは、化学工学における単位操作の一つである。この原理を使用し何らかの液体の混合物から何らかの成分を蒸留することをフラッシュ蒸留という。
より熱効率を向上させた、フラッシュ蒸留である多段フラッシュ蒸留 (MSF:Multi-Stage Flash)は海水淡水化に広く利用されている。
単一成分液体のフラッシュ蒸発
編集単一成分の液体のフラッシュ蒸発は、等エンタルピープロセスであり、しばしば断熱フラッシュと呼ばれる。 次の方程式は、スロットルバルブまたはデバイス周辺の単純な熱収支から導き出され、単一成分の液体の気化量を予測するために使用される。
上記の方程式に必要なエンタルピーデータが利用できない場合は、次の方程式を使用できる。
多成分液体の平衡フラッシュ
編集多成分液体の平衡フラッシュは、単一の平衡段階を使用した単純な蒸留プロセスとして視覚化できる。 これは、単一成分液体のフラッシュ蒸発とは大きく異なり、複雑で 多成分液体の場合、フラッシュ蒸気と残留液体の量を所定の温度と圧力で互いに平衡にして計算するには、試行錯誤の反復解が必要であり、 このような計算は、一般に平衡フラッシュ計算と呼ばれている。 Rachford-Rice方程式を解くことがある: [5] [6] [7] [8]
最も重要なのは間違いなく温度だが、平衡定数K iは一般に多くのパラメーターの関数である。それらは次のように定義される。
Rachford-Rice方程式がβについて解かれると、成分x iおよびy iは次のようにすぐに計算できる。
Rachford-Rice方程式は、 βの複数の解を持つことができる。その1つがすべてのx iとy iが正になることを保証する。 特に、 βが1つしかない場合:
噴霧乾燥との対比
編集噴霧乾燥はフラッシュ蒸発の一形態と見られることがある。 しかし、液体蒸発の一形態ではあるが、フラッシュ蒸発とはまったく異なる。 噴霧乾燥では、非常に小さな固体のスラリーを高温のガス中に懸濁させることで急速に乾燥させる。 スラリーはまずエアロゾル化され、非常に小さな液滴となり、高温の乾燥空気中に噴霧される。 液体は急速に蒸発し、乾燥粉末または乾燥固体顆粒が残る。 乾燥粉末または固体顆粒は、サイクロン、ろ過、または電気集塵を使用して排気から回収される。
自然なフラッシュ蒸発
編集この節には内容がありません。 (2020年11月) |
脚注
編集- ^ a b フラッシュ蒸留 - 『栄養・生化学辞典』朝倉書店(コトバンク)
- ^ Stanley M. Walas (1988). Chemical Process Equipment:Selection and Design. Butterworth-Heinemann. ISBN 0-409-90131-8
- ^ Gas Processing Suppliers Association (GPSA) (1987). Engineering Data Book (10th Edition, Vol. 1 ed.). Gas Processing Suppliers Association, Tulsa, Oklahoma
- ^ Vic Marshall; Steve Ruhemann (2001). Fundamentals of Process Safety. IChemE. p. 46
- ^ Harry Kooijman and Ross Taylor (2000). The ChemSep Book (2nd ed.). ISBN 3-8311-1068-9 See page 186.
- ^ Analysis of Objective Functions (Pennsylvania State University)
- ^ Flash Calculations using the Soave-Redlich-Kwong equation of state (view full-size image)
- ^ Curtis H. Whitson, Michael L. Michelsen, The Negative Flash, Fluid Phase Equilibria, 53 (1989) 51–71.
関連項目
編集外部リンク
編集- 蒸気とフラッシュスチームのアニメーション、写真、およびフラッシュスチームと蒸気化されたフラクションの違いの技術的な説明。
- フラッシュスチームチュートリアルフラッシュスチームを回復するメリット、その方法と一般的なアプリケーション。
- 中東および西アジアの水淡水化技術
- 噴霧乾燥の議論
- フラッシュ蒸発プログラムオンライン炭化水素化合物のフラッシュ蒸留。