パース・クインカンシャル図法

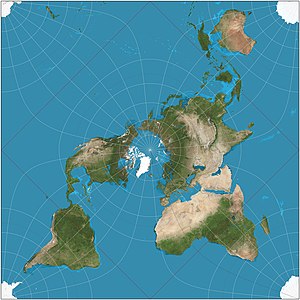
パース・クインカンシャル図法（パース・クインカンシャルずほう、英語: Peirce quincuncial projection）とは、地図投影法の一種で、球面を正方形に投影する、有限個の点を除き正角な図法である。1879年、アメリカ沿岸測地局（現在のアメリカ海洋大気庁国立測地測量局と沿岸測量部の前身）に在籍していたチャールズ・サンダース・パースが、en:Schwarz–Christoffel mappingを元にして考案した。

パース・クインカンシャル図法

投影式

まず、北半球が複素平面上の単位円内となる平射図法により、球面から複素平面へ投影する。その上で、この複素平面上の $r$ が $w$ に写像されるとき、ヤコビの楕円関数で表すと、

$\operatorname {sd} \left({\sqrt {2}}w,1/{\sqrt {2}}\right)={\sqrt {2}}r$

の関係が成り立つ。つまり

$w=\int ^{r}{\frac {{\rm {d}}z}{\sqrt {1-z^{4}}}}$

なる写像である。

特徴

パース・クインカンシャル図法におけるテイソーの指示楕円

この図法は特異点以外のすべてで正角になる。特異点は、定義域の複素平面上では±1と$\pm i$、北極を中心とした場合は赤道上に90度間隔の4点である。地図上では赤道が正方形となり、折れ曲がる点が特異点に対応する。特異点においては360度が180度に「均等に圧縮」されるので、特異点を中心としてテイソーの指示楕円を描くと正しい半円が描かれるが、正しい円ではない。少しずれた位置から特異点を含む円を投影すると明らかに歪む。

平面充填を施したパース・クインカンシャル図法

この図法では球面全体が正方形の中に納まる。外周に切れ目が出来るが、繰り返し構造を持っており、連続してタイル状に並べることができる（ただし特異点の周辺では、同じものがすぐ近くに2回描かれる）。図法名にあるquincuncialはサイコロの五の目のような正方形構造を指す。そのため斜軸法などを使わなくても、大陸を分断しないような形に切り抜くことなどもできる。

同様の手法を用いた図法に、この図法の横軸法であるen:Adams hemisphere-in-a-square projection、斜軸法であるen:Guyou hemisphere-in-a-square projectionがあり、その他にも正三角形（en:Lee conformal world in a tetrahedron）など他の多角形に投影する図法がある。

関連項目

• レムニスケート楕円関数

参考文献

• Peirce, C.S. (1879). “A quincuncial projection of the sphere”. American Journal of Mathematics 2 (4): 394–396. 
• Snyder, John P. (1989). An Album of Map Projections, Professional Paper 1453. US Geological Survey. pp. 190, 236. http://pubs.usgs.gov/pp/1453/report.pdf