シュードノット
シュードノット(英: pseudoknot)は、少なくとも2つのステムループ構造を含む核酸の二次構造で、一方のステムの片側が他方のステムの間に位置している。シュードノットは、1982年にカブ黄斑モザイクウイルスのRNA中に初めて同定された[2]。結び目(ノット)に似た三次構造へ折り畳まれるが、実際には結び目ではない。

予測と同定
編集シュードノットの構造形態は、コンテクスト依存性や塩基対形成領域の重複のため、計算生物学的手法による検出には適していない。シュードノット中の塩基対形成パターンは入れ子状になっておらず、このことが標準的な動的計画法によるRNA配列中のシュードノットの存在予測をより困難なものにしている。動的計画法では塩基対形成したステムを同定するために再帰的なスコアリングシステムが用いられるため、入れ子状になっていない塩基対はほとんど検出することができない。確率文脈自由文法といった新たな手法もシュードノットを同様の問題を抱えている。そのため、MfoldやPfoldといったよく用いられる二次構造予測手法ではクエリ配列中に存在するシュードノット構造を予測することはできず、2つのステムの内より安定なものだけが同定される。
動的計画法を用いて限られたクラスのシュードノットを同定することは可能であるが、これらの手法は網羅的ではなく、シュードノットを考慮しないアルゴリズムよりも配列長に応じた計算規模の増大が著しい[3][4]。シュードノットを含む最小自由エネルギー構造の予測はNP完全問題であることが示されている[5][6]。
生物学的意義
編集いくつかの重要な生物学的過程がシュードノットを形成するRNA分子に依存しており、その多くは広範囲にわたる三次構造を有するものである。リボヌクレアーゼPのシュードノット領域は、全ての進化の過程で最も保存されているエレメントの1つである。テロメラーゼRNAのシュードノットはテロメラーゼ活性に重要である[1]。いくつかのウイルスは、宿主細胞に進入するためにシュードノット構造を用いてtRNAに似たモチーフを形成する[7]。
表記法
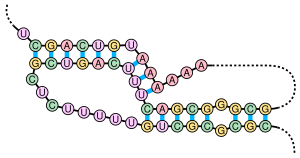
編集シュードノットは一次配列上でどのようにステムが交差するか、そして何度交差するかによって多数のタイプが存在する。この違いによって、シュードノットはH、K、L、M型へと分類されている[8]。冒頭の図で示されている単純なテロメラーゼP2b-P3は、H型のシュードノットである。
RNAの二次構造は通常ドットとブラケットによる表記がなされ、丸括弧 () はステムを形成する塩基対を、ドットはループを表す。しかし、シュードノットではステムが他のステムによって分断されているため、異なるステムを表すために他のブラケットまたは文字を用いた表記の拡張が必要である。そのような場合、ステムの開始には ([{<ABCDE 、終わりには edcba>}]) が外側から順番に用いられる[9]。2つの(わずかに異なる)テロメラーゼのアラインメントをこの表記法で示すと次のようになる。
(((.(((((........[[[[[[[[[))))).))). ...]]].]]]]]].
drawing 1 CGCGCGCUGUUUUUCUCGCUGACUUUCAGCGGGCGA---AAAAAAUGUCAGCU 50
ALIGN |.||||||||||||||||||||||||| .|.| |||||| ||||||.
1ymo 1 ---GGGCUGUUUUUCUCGCUGACUUUCAGC--CCCAAACAAAAAA-GUCAGCA 47
((((((........[[[[[[[[[)))) ))........]]].]]]]]].
テロメラーゼRNAのシュードノットに通常存在するUバルジが、シュードノットの安定性を増すために1ymoでは除かれている[10]。
出典
編集- ^ a b Chen, JL; Greider, CW (7 June 2005). “Functional analysis of the pseudoknot structure in human telomerase RNA.”. Proceedings of the National Academy of Sciences of the United States of America 102 (23): 8077–9. Bibcode: 2005PNAS..102.8080C. doi:10.1073/pnas.0502259102. PMC 1149427. PMID 15849264.
- ^ “Pseudoknots: RNA structures with diverse functions”. PLoS Biol. 3 (6): e213. (June 2005). doi:10.1371/journal.pbio.0030213. PMC 1149493. PMID 15941360.
- ^ Rivas, E.; Eddy, S. R. (1999-02-05). “A dynamic programming algorithm for RNA structure prediction including pseudoknots”. Journal of Molecular Biology 285 (5): 2053–2068. doi:10.1006/jmbi.1998.2436. ISSN 0022-2836. PMID 9925784.
- ^ Dirks, Robert M.; Pierce, Niles A. (2004-07-30). “An algorithm for computing nucleic acid base-pairing probabilities including pseudoknots”. Journal of Computational Chemistry 25 (10): 1295–1304. doi:10.1002/jcc.20057. ISSN 0192-8651. PMID 15139042.
- ^ Lyngsø, R. B.; Pedersen, C. N. (2000). “RNA pseudoknot prediction in energy-based models”. Journal of Computational Biology: A Journal of Computational Molecular Cell Biology 7 (3-4): 409–427. doi:10.1089/106652700750050862. ISSN 1066-5277. PMID 11108471.
- ^ Lyngsø, R. B. (2004). Complexity of pseudoknot prediction in simple models. Paper presented at the ICALP.
- ^ “A new principle of RNA folding based on pseudoknotting.”. Nucleic Acids Res 13 (5): 1717–31. (1985). doi:10.1093/nar/13.5.1717. PMC 341107. PMID 4000943.
- ^ Kucharík, M; Hofacker, IL; Stadler, PF; Qin, J (15 January 2016). “Pseudoknots in RNA folding landscapes.”. Bioinformatics (Oxford, England) 32 (2): 187–94. doi:10.1093/bioinformatics/btv572. PMC 4708108. PMID 26428288.
- ^ Antczak, M; Popenda, M; Zok, T; Zurkowski, M; Adamiak, RW; Szachniuk, M (15 April 2018). “New algorithms to represent complex pseudoknotted RNA structures in dot-bracket notation.”. Bioinformatics (Oxford, England) 34 (8): 1304–1312. doi:10.1093/bioinformatics/btx783. PMC 5905660. PMID 29236971.
- ^ Theimer, CA; Blois, CA; Feigon, J (4 March 2005). “Structure of the human telomerase RNA pseudoknot reveals conserved tertiary interactions essential for function.”. Molecular Cell 17 (5): 671–82. doi:10.1016/j.molcel.2005.01.017. PMID 15749017.